สวัสดีคร้าบบ^^ ในโพสต์นี้พี่หมอแม็คจะมาพูดเกี่ยวกับเรขาคณิตวิเคราะห์และภาคตัดกรวย ซึ่งเป็นพื้นฐานสำคัญในการมองเป็นภาพของกราฟ และต้องนำเรื่องนี้ไปประยุกต์ใช้ต่ออีกหลายเรื่องที่จะกล่าวถึงต่อไป พี่หมอแม็คได้สรุปเนื้อหาไว้ในโพสต์นี้โพสต์เดียวแล้วนะครับ นอกจากนี้ยังมีเทคนิคการทำข้อสอบเล็ก ๆ น้อย ๆ มาฝากกันคั้บบ

เรขาคณิตวิเคราะห์

เรขาคณิตวิเคราะห์ (geometric analytic) เป็นการวิเคราะห์รูปเรขาคณิตที่อยู่บนระนาบ ได้แก่ การหาระยะทางหรือความยาวของจุดสองจุด การหาจุดกึ่งกลาง การหาระยะทางระหว่างจุดกับเส้นตรง การหาระยะทางระหว่างเส้นตรงสองเส้น

Ex.1 จงหาระยะทางระหว่างจุด $P(2,3)$ และ $Q(-2,0)$

วิธีทำ

ระยะทางระหว่างจุด $P(2,3)$ และ $Q(-2,0)$ เท่ากับ

\begin{align*} PQ &= \sqrt{(2-(-2))^2+(3-0)^2}\\ &= \sqrt{4^2+3^2}\\ &= \sqrt{16+9}\\ &= \sqrt{25}\\ &= 5 \end{align*}

Ex.2 จงหาจุดกึ่งกลางระหว่างจุด $P(2,3)$ และ $Q(-2,0)$

วิธีทำ

จุดกึ่งกลางระหว่างจุด $P$ และ $Q$ มีตำแหน่งเป็น

\begin{align*} \left( \frac{2+(-2)}{2},\ \frac{3+(0)}{2} \right) = \left( \frac{0}{2},\ \frac{3}{2} \right) = (0,\ 1.5) \end{align*}

Ex.3 จงหาสมการเส้นตรงที่ผ่านจุด $P(2,3)$ และ $Q(-2,0)$

วิธีทำ

เนื่องจากความชันของเส้นตรงที่ผ่านจุด $P(2,3)$ และ $Q(-2,0)$ เท่ากับ $\displaystyle m = \frac{3-0}{2-(-2)} = \frac{3}{4}$
ดังนั้น สมการเส้นตรงที่ผ่านจุด $P(2,3)$ และ $Q(-2,0)$ คือ สมการ

\begin{align*} y - y_1 &= m(x - x_1) \\ y - 0 &= \frac{3}{4} (x-(-2)) \\ y &= \frac{3}{4}x + \frac{3}{2} \end{align*}

Ex.4 จงหาระยะตัดแกน $Y$ ของสมการเส้นตรงที่มีความชันเท่ากับ $2$ และผ่านจุด $(3, 5)$

วิธีทำ

เนื่องจากสมการเส้นตรงในรูปมาตรฐาน คือ $y - y_1 = m(x - x_1)$
ดังนั้น สมการเส้นตรงที่มีความชันเท่ากับ $2$ และผ่านจุด $(3, 5)$ คือ สมการ

\begin{align*} y - y_1 &= m(x - x_1) \\ y - 5 &= 2 (x-3) \\ y &= 2x - 1 \end{align*}

พิจารณาหาระยะตัดแกน $Y$
ให้ $x=0$ จะได้ว่า $y = 2(0) - 1 = -1$
เพราะฉะนั้น ระยะตัดแกน $Y$ เท่ากับ $-1$

ต่อไปพี่แม็คจะให้น้อง ๆ พิจารณาเส้นตรง $2$ เส้นต่อไปนี้
Ex.5 จงวาดกราฟของเส้นตรงต่อไปนี้

\begin{align*} L &: y = 2x + 4 \\ \ell_1 &: y = 2x - 2\\ \ell_2 &: y = -\frac{1}{2}x + 2\\ \ell_3 &: y = -2x + 2 \end{align*}

พร้อมพิจารณาว่า เส้นตรง $L$ กับเส้นตรง $\ell_1, \ell_2, \ell_3$ ขนานกันหรือตั้งฉากกัน

วิธีทำ

เมื่อวาดกราฟของเส้นตรง $L$ กับเส้นตรง $\ell_1$ ได้เป็นดังนี้

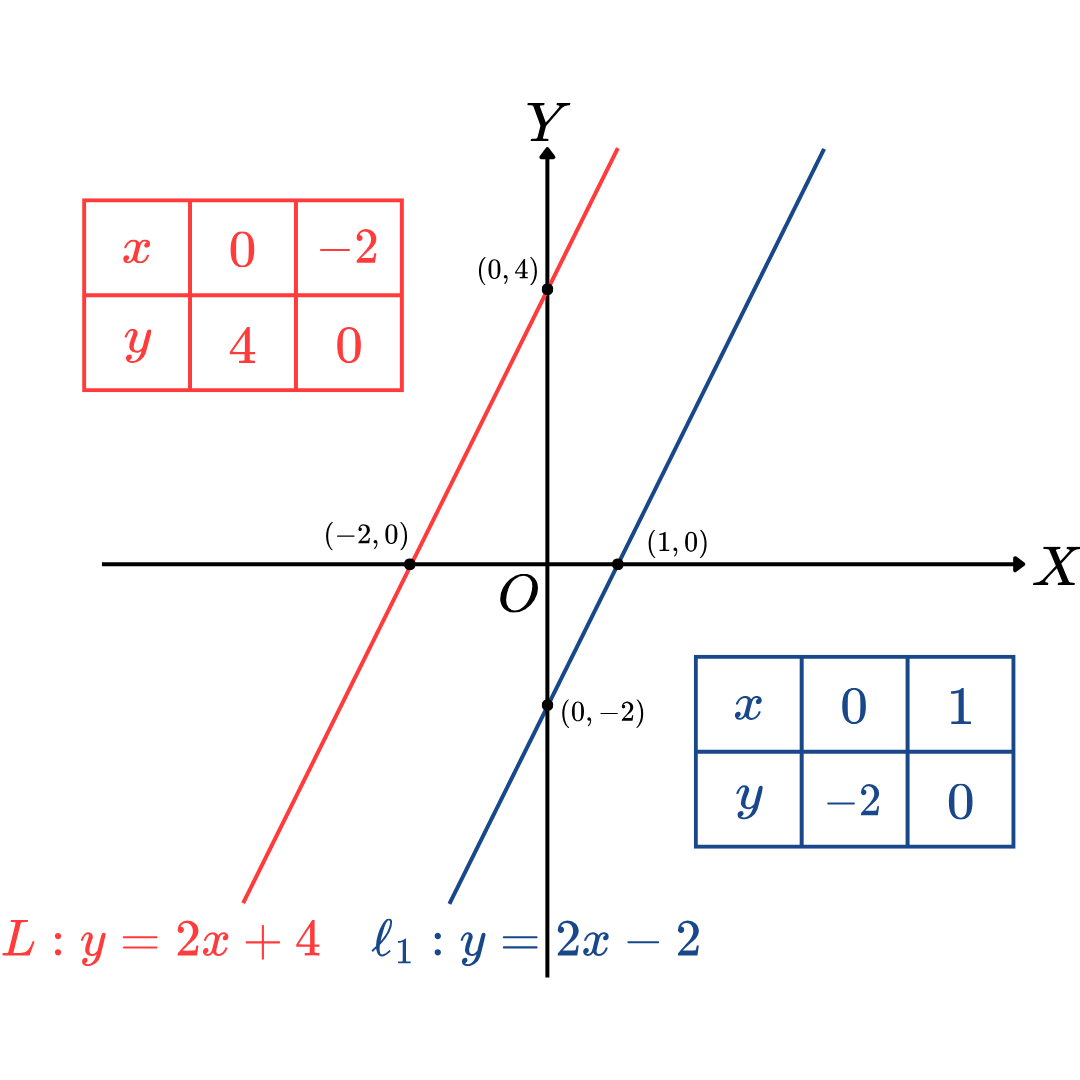
เห็นว่า เส้นตรง $L$ กับเส้นตรง $\ell_1$ ขนานกัน
เมื่อวาดกราฟของเส้นตรง $L$ กับเส้นตรง $\ell_2$ ได้เป็นดังนี้

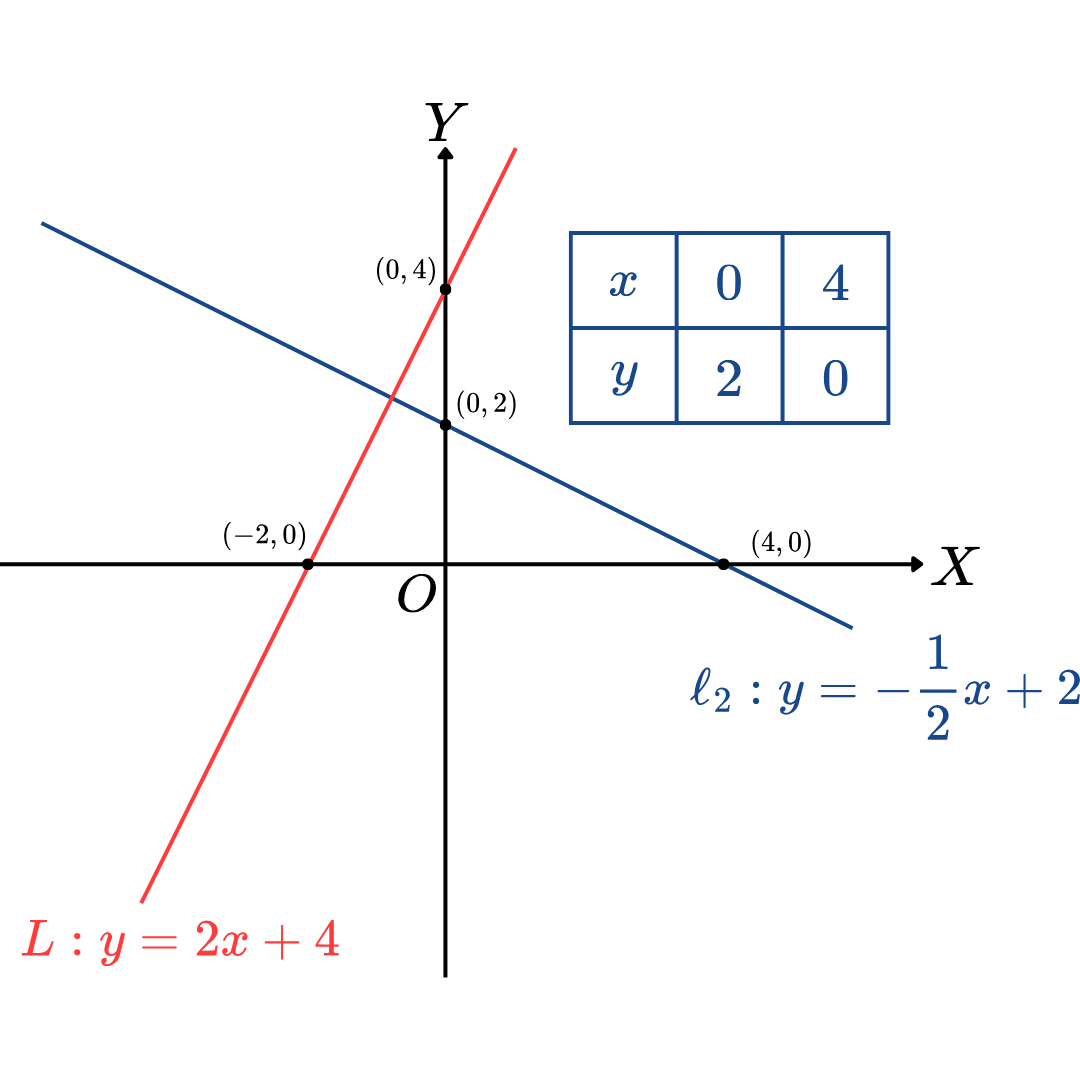
เห็นว่า เส้นตรง $L$ กับเส้นตรง $\ell_2$ ตั้งฉากกัน
เมื่อวาดกราฟของเส้นตรง $L$ กับเส้นตรง $\ell_3$ ได้เป็นดังนี้

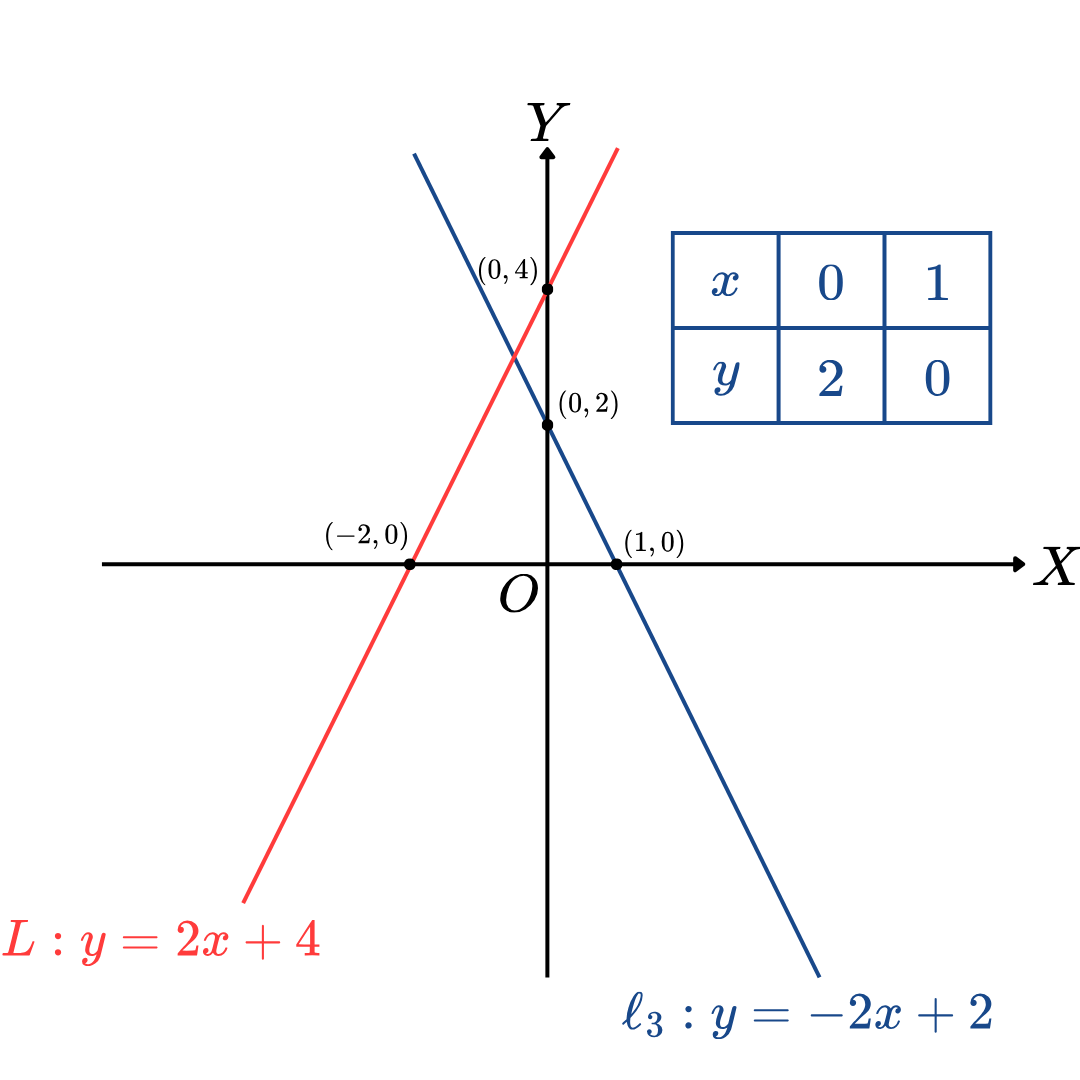
เห็นว่า เส้นตรง $L$ กับเส้นตรง $\ell_3$ ไม่ขนานกัน และไม่ตั้งฉากกัน

ซึ่งพี่แม็คสรุปความสัมพันธ์ของเส้นตรง ได้ดังนี้
ให้ $\ell_1: y=m_1x+c_1$ และ $\ell_2: y=m_2x+c_2$ เป็นสมการเส้นตรง
เส้นตรง $\ell_1$ ขนานกับ $\ell_2$ ก็ต่อเมื่อ $m_1 = m_2$
เส้นตรง $\ell_1$ ตั้งฉากกับ $\ell_2$ ก็ต่อเมื่อ $m_1 m_2 = -1$

Ex.6 จงหาระยะทางระหว่างจุด $(4,-3)$ และเส้นตรง $5x-3=12(y-1)$

วิธีทำ

เนื่องจากเส้นตรง $5x-3=12(y-1)$ จัดรูปใหม่ให้อยู่ในรูปทั่วไปได้เป็น $5x - 12y + 9 = 0$
ดังนั้น ระยะทางระหว่างจุด $(-2,4)$ และเส้นตรง $5x - 12y + 9 = 0$ เท่ากับ
$\displaystyle\frac{\left| 5(4) -12(-3)+9\right|}{\sqrt{5^2+12^2}} = \frac{65}{13} = 5$ หน่วย

Ex.7 จงหาสมการเส้นตรงที่ขนานกับเส้นตรง $4 - x = 5 + y$ ที่ห่างกัน $4$ หน่วย

วิธีทำ

จากเส้นตรง $4 - x = 5 + y$ จัดรูปใหม่ให้อยู่ในรูปทั่วไปได้เป็น $x + y + 1 = 0$
กำหนดให้ $L: x + y + 1 = 0$ เป็นเส้นตรงจากโจทย์ และให้ $\ell: x+y+c=0$ เป็นเส้นตรงที่ขนานกับเส้นตรง $L$ เมื่อ $c$ เป็นจำนวนจริง
ให้ $d$ เป็นระยะทางระหว่างเส้นตรง $L$ ที่ขนานกับเส้นตรง $\ell$ ที่ห่างกัน $4$ หน่วย
จะได้ว่า $\displaystyle d = \frac{\left| 1 - c \right|}{\sqrt{1^2+1^2}}$ นั่นคือ $4\sqrt{2} = \left| 1 - c \right|$
ทำให้ได้ว่า $1-c = 4\sqrt{2}$ หรือ $1-c = -4\sqrt{2}$ \ นั่นคือ $c= 1-4\sqrt{2}$ หรือ $c= 1+4\sqrt{2}$
ดังนั้น สมการเส้นตรงที่ขนานกับเส้นตรง $4 - x = 5 + y$ ที่ห่างกัน $4$ หน่วย คือ
สมการ $x + y + (1-4\sqrt{2}) = 0$ และ $x + y + (1+4\sqrt{2}) = 0$

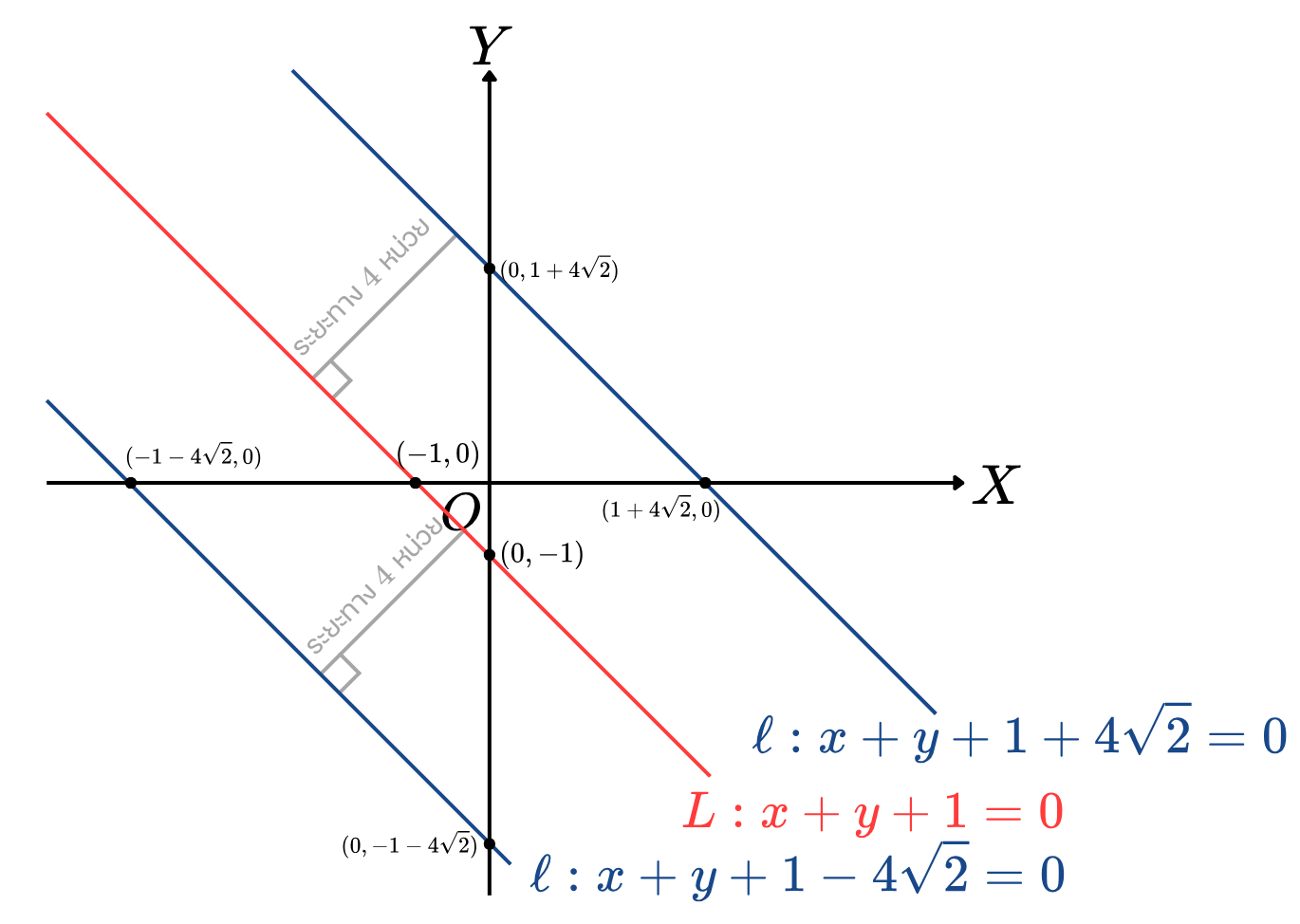
ภาคตัดกรวย

ภาคตัดกรวย (conic section) เป็นการหาภาพการตัดของกรวยกลมตรงในระนาบต่าง ๆ ที่แตกต่างกัน ซึ่งภาพการตัดที่ได้จะมีได้แก่ วงกลม วงรี ไฮเพอร์โบลา และพาราโบลา

วงกลม

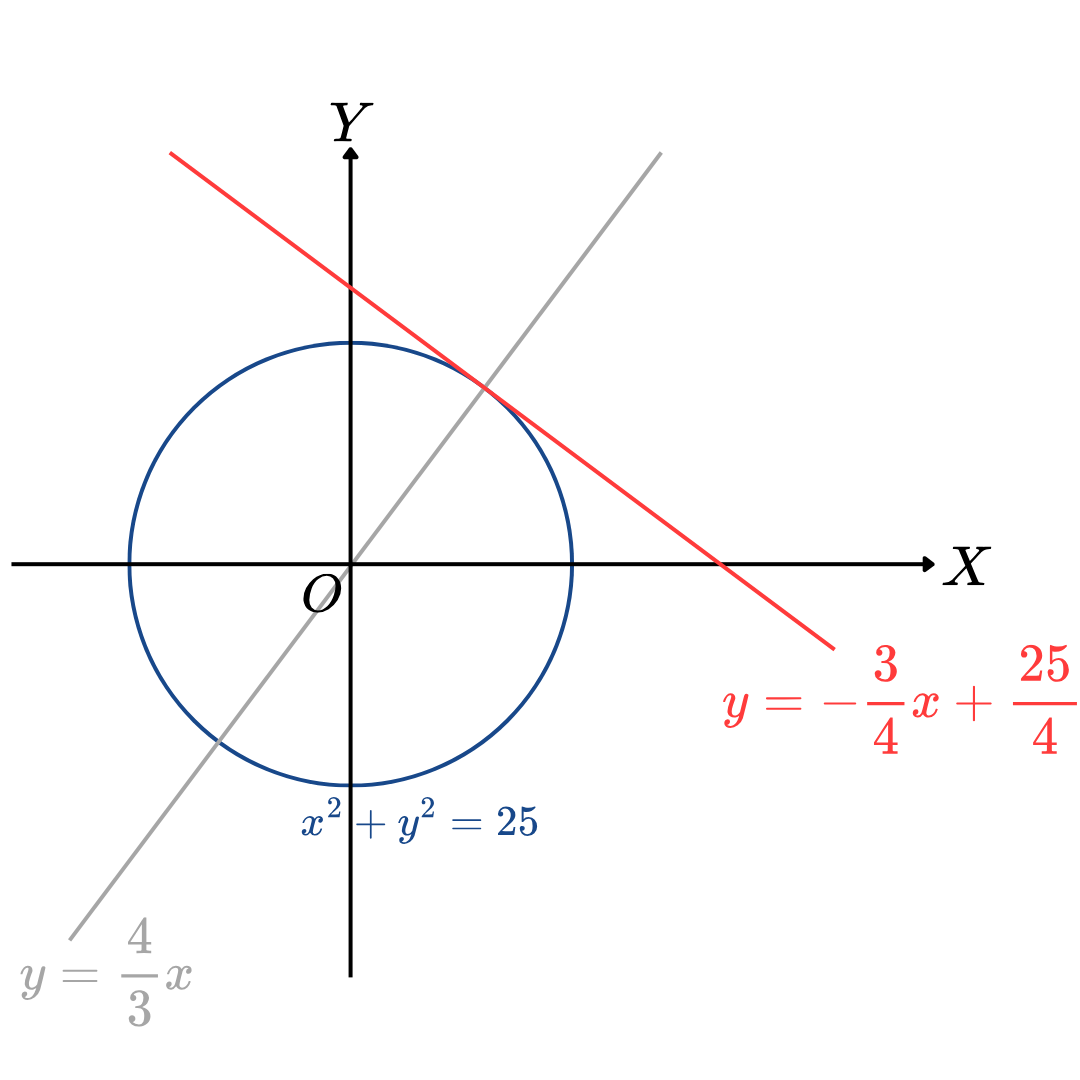
Ex.8 จงหาสมการเส้นสัมผัสของวงกลม $x^2 +y^2 = 25$ ที่จุด $(3, 4)$

วิธีทำ

ความชันของเส้นตรงที่ผ่านจุด $(0,0)$ และ $(3,4)$ เท่ากับ $\displaystyle \frac{4-0}{3-0} = \frac{4}{3}$
จะได้ว่า สมการเส้นตรงที่ผ่านจุด $(0,0)$ และ $(3,4)$ คือ สมการ $y = \frac{4}{3} x$
ให้ $m$ เป็นความชันของเส้นตรงที่ตั้งฉากกับ $\displaystyle y = \frac{4}{3} x$ จะได้ว่า $\displaystyle m\cdot \frac{4}{3} = -1$ นั่นคือ $m = -\frac{3}{4}$
ต่อไปจะหาสมการเส้นตรงที่ตั้งฉากกับ $y = \frac{4}{3} x$ ที่ผ่านจุด $(3, 4)$ ดังนี้

\begin{align*} y - y_1 &= m(x - x_1) \\ y - 4 &= -\frac{3}{4} (x-3) \\ y &= -\frac{3}{4}x + \frac{25}{4} \end{align*}

ดังนั้น สมการเส้นสัมผัสของวงกลม $x^2 +y^2 = 25$ ที่จุด $(3, 4)$ คือ สมการ $\displaystyle y = -\frac{3}{4}x + \frac{25}{4}$

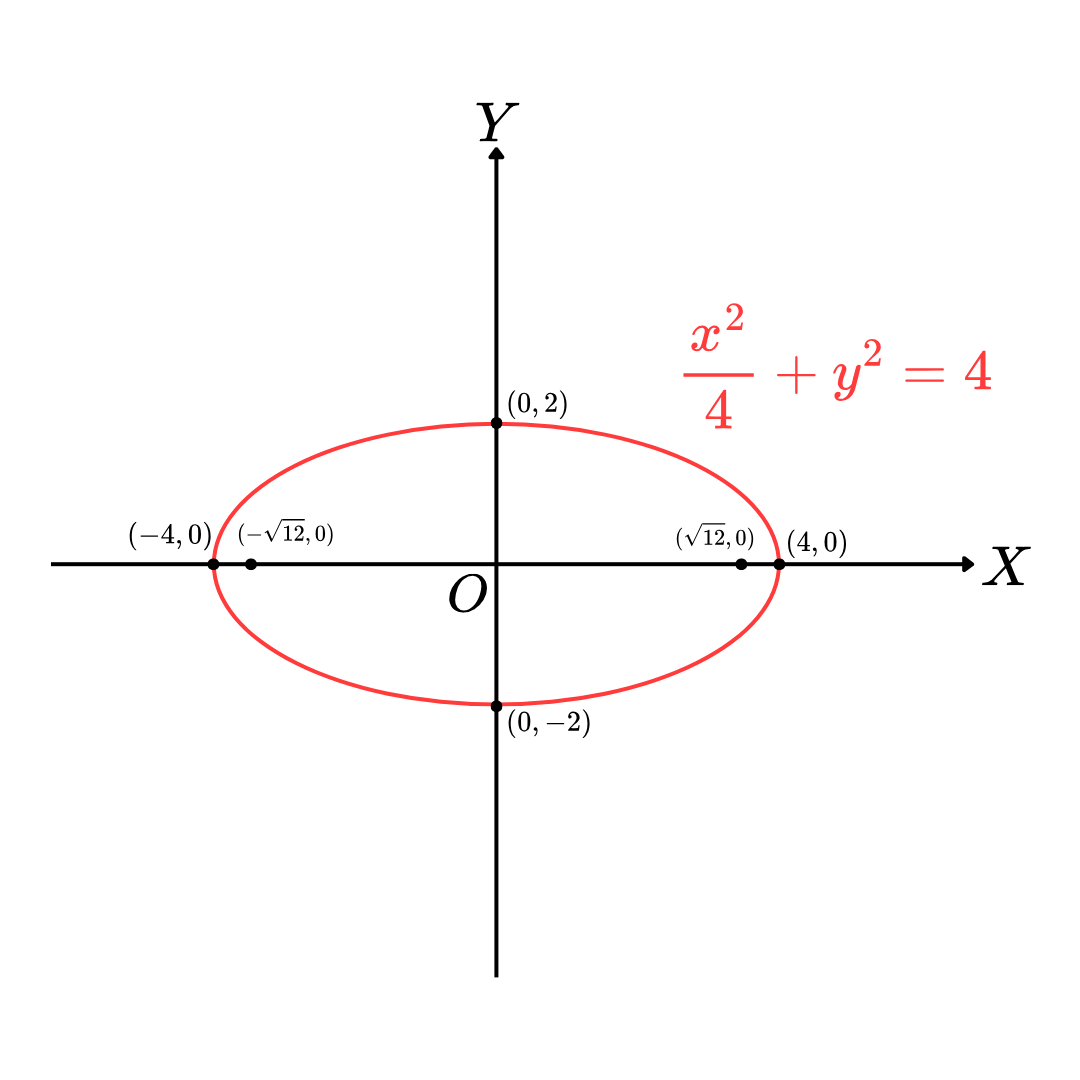
Ex.9 จงหาจุดยอด ความยาวแกนเอก จุดปลายแกนโท ความยาวแกนโท และจุดโฟกัสของวงรี $\displaystyle \frac{x^2}{4} +y^2 = 4$

วิธีทำ

จากวงรี $\displaystyle \frac{x^2}{4} +y^2 = 4$ จัดรูปใหม่ได้เป็น $\displaystyle \frac{x^2}{16} + \frac{y^2}{4} = 1$
พิจารณาหาจุดยอดและความยาวแกนเอก โดยให้ $y=0$ จะได้ว่า

\begin{align*} \frac{x^2}{16} + \frac{0^2}{4} &= 1 \\ x^2 &= 16 \\ x^2-16 &= 0 \\ (x-4)(x+4) &= 0 \\ x &= 4, -4 \end{align*}

ดังนั้น จุดปลายแกนเอกหรือจุดยอด คือ จุด $(4,0)$ และ $(-4,0)$
ทำให้ความยาวแกนเอกเท่ากับ $\sqrt{(4-(-4))^2} = 8$ หน่วย
ต่อไปจะหาจุดปลายแกนโทและความยาวแกนโท โดยให้ $x=0$ จะได้ว่า

\begin{align*} \frac{0^2}{16} + \frac{y^2}{4} &= 1 \\ y^2 &= 4 \\ y^2-4 &= 0 \\ (y-2)(y+2) &= 0 \\ y &= 2, -2 \end{align*}

ดังนั้น จุดปลายแกนโท คือ จุด $(0,2)$ และ $(0,-2)$
ทำให้ความยาวแกนโทเท่ากับ $\sqrt{(2-(-2))^2} = 4$ หน่วย
ต่อไปจะหาจุดโฟกัส เนื่องจากจุดโฟกัสอยู่ที่จุด $(c,0)$ และ $(-c,0)$ เมื่อ $a^2 - b^2 = c^2$
นั่นคือ $a^2 - b^2 = 16 - 4 = 12 = c^2$ ดังนั้น $c = \sqrt{12}$
เพราะฉะนั้น จุดโฟกัส คือ จุด $(\sqrt{12},0)$ และ $(-\sqrt{12},0)$

สำหรับวงรีดังกล่าวเป็นวงรีที่รีตามแกน $X$ และมีวงรีอีกรูปแบบหนึ่งที่รีตามแกน $Y$ เขียนในรูปมาตรฐานได้เป็น

\begin{align*} \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 \end{align*}

เมื่อ $a>b>0$ โดยแกนเอกอยู่บนแกน $Y$ ส่วนแกนโทอยู่บนแกน $X$ และจุดโฟกัสอยู่ที่ $(0,c)$ และ $(0,-c)$

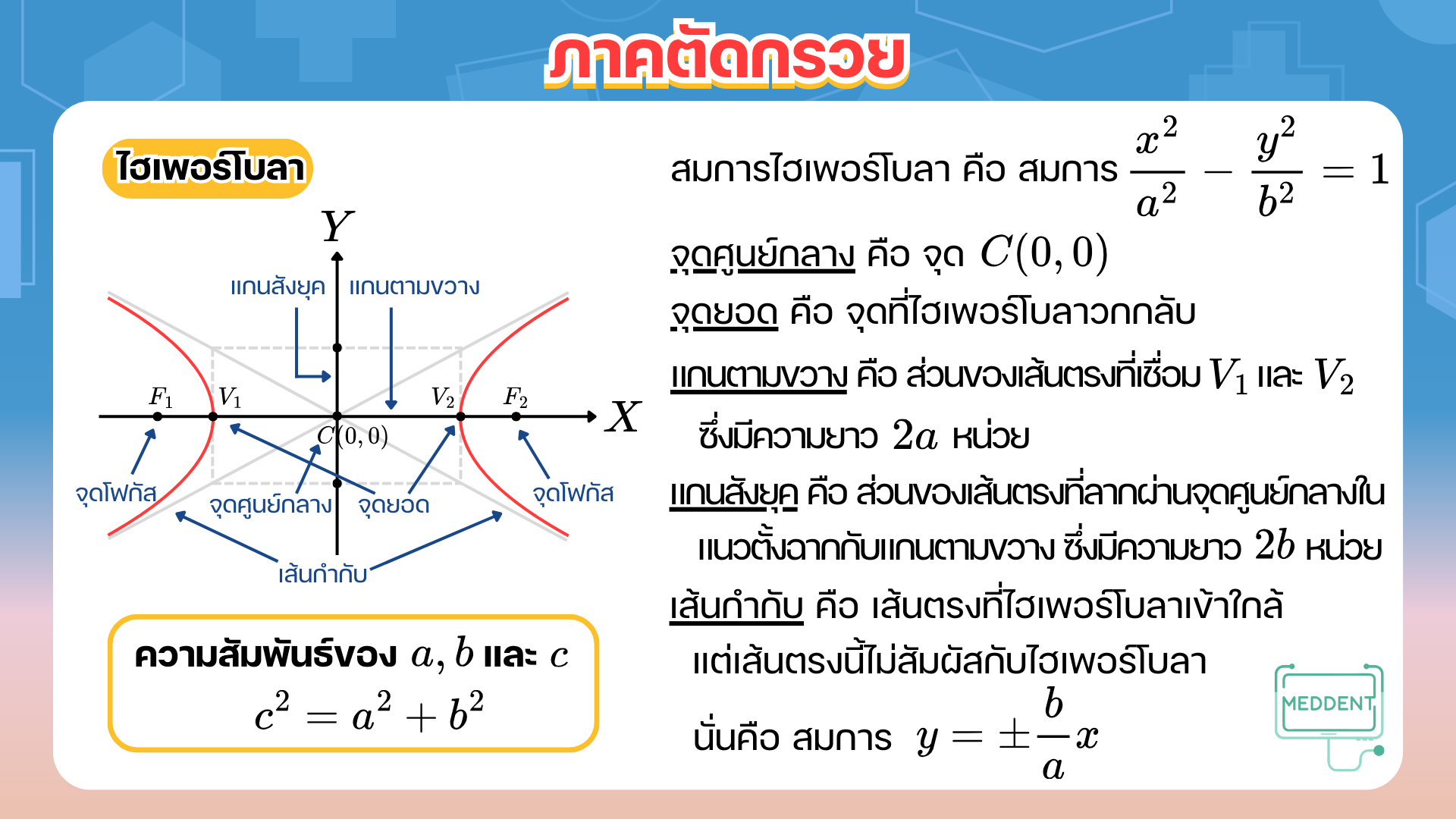
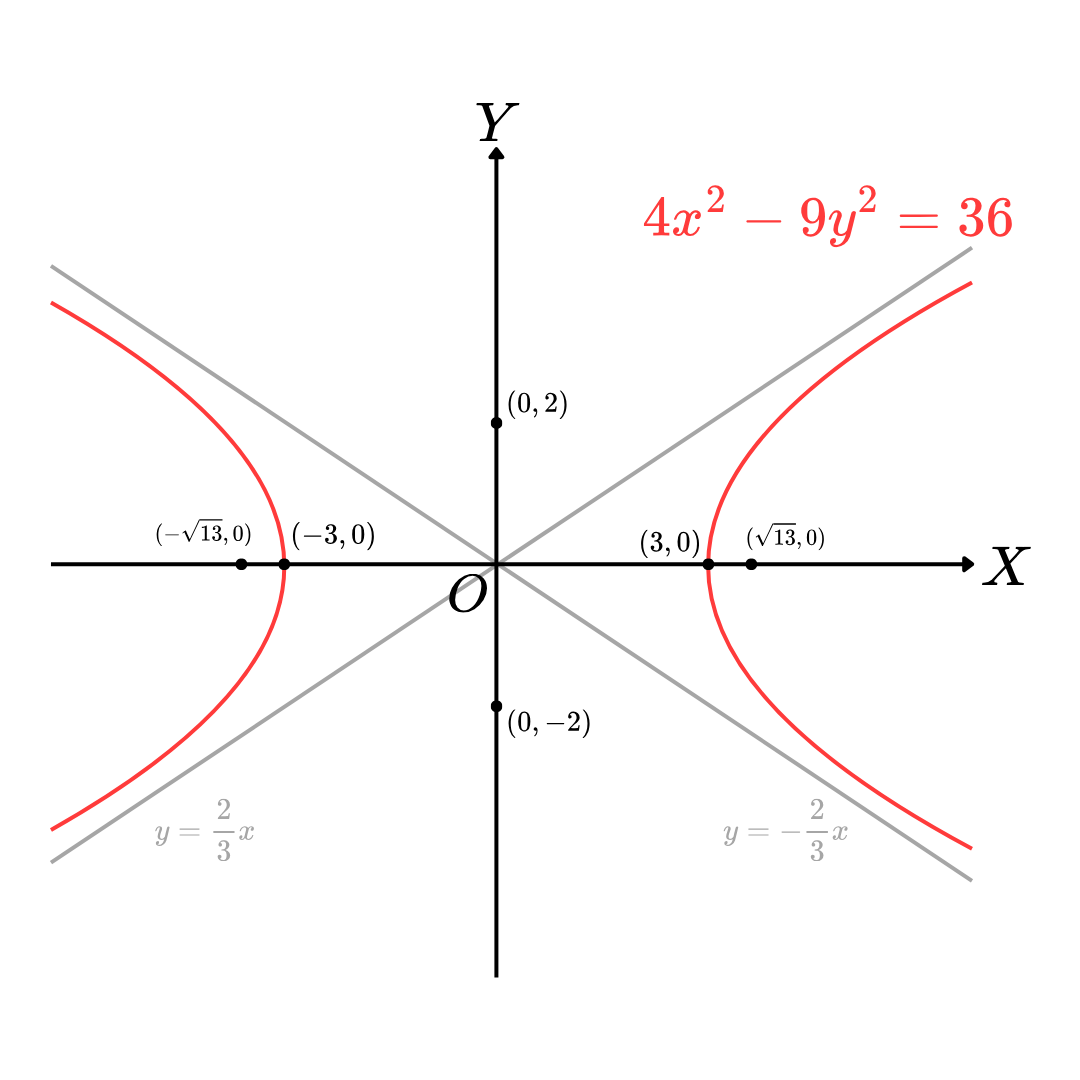
Ex.10 จงหาจุดยอด ความยาวแกนตามขวาง ความยาวแกนสังยุค เส้นกำกับ และจุดโฟกัสของไฮเพอร์โบลา $4x^2 - 9y^2 = 36$

วิธีทำ

เนื่องจากไฮเพอร์โบลาในรูปมาตรฐาน คือ $\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ เมื่อ $a$ และ $b$ เป็นจำนวนจริงบวก
จะได้ว่า ไฮเพอร์โบลา $4x^2 - 9y^2 = 36$ สามารถจัดรูปใหม่ได้เป็น $\displaystyle \frac{x^2}{9} - \frac{y^2}{4} = 1$
(นั่นคือ $a=3$ และ $b=2$ )
ดังนั้น จุดยอด คือ จุด $(a,0)$ และ $(-a,0)$ นั่นคือ $(3,0)$ และ $(-3,0)$
แกนตามขวางยาว $2a = 6$ หน่วย และแกนสังยุคยาว $2b = 4$ หน่วย
เส้นกำกับ คือ สมการ $\displaystyle y = \frac{2}{3} x$ และ $\displaystyle y = -\frac{2}{3} x$
เนื่องจาก $c^2 = a^2 + b^2$ จะได้ว่า $c=\sqrt{3^2+2^2} = \sqrt{13}$
ดังนั้น จุดโฟกัส จุด $(c,0)$ และ $(-c,0)$ นั่นคือ จุด $(\sqrt{13}, 0)$ และ $(-\sqrt{13}, 0)$

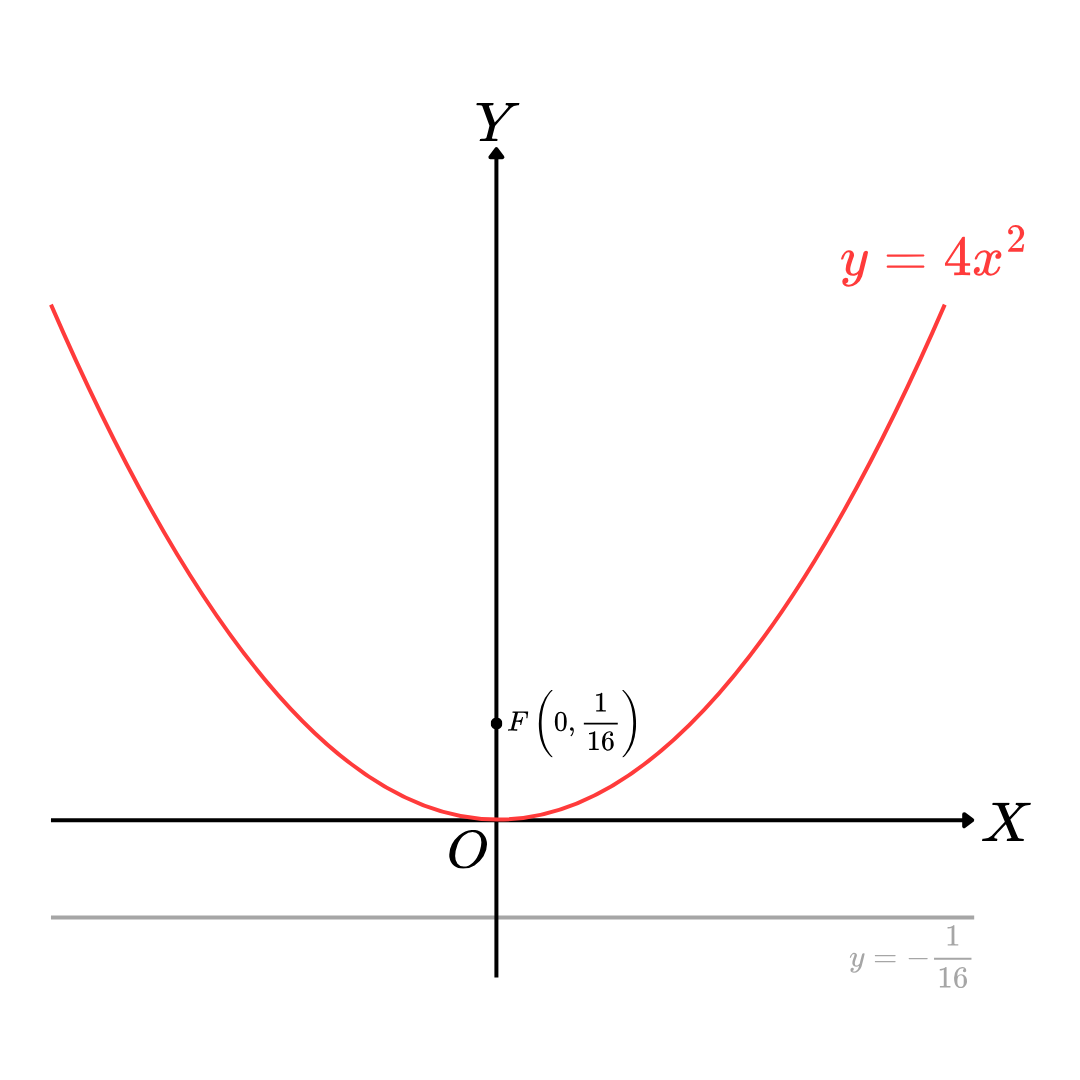
Ex.11 จงหาความยาวลาตัสเรคตัม ไดเรกตริกซ์ และจุดโฟกัสของพาราโบลา $y = 4x^2$

วิธีทำ

เนื่องจากพาราโบลาในรูปมาตรฐาน คือ $x^2 = 4py$ เมื่อ $p$ เป็นจำนวนจริงที่ไม่ใช่ $0$
จะได้ว่า พาราโบลา $y = 4x^2$ สามารถจัดรูปใหม่ได้เป็น $\displaystyle x^2 = \frac{1}{4} y$ นั่นคือ $\displaystyle x^2 = 4 \left(\frac{1}{16}\right) y$
เพราะฉะนั้น $\displaystyle p=\frac{1}{16}$
ดังนั้น ลาตัสเรคตัมยาว $\displaystyle\left|2p\right| = \left|2 \cdot \frac{1}{16}\right| = \frac{1}{8}$ หน่วย
ไดเรกตริกซ์ คือ สมการ $y = -p$ นั่นคือ สมการ $\displaystyle y = -\frac{1}{16}$
และจุดโฟกัส จุด $(0,p)$ นั่นคือ จุด $\left(0, \frac{1}{16}\right)$

ข้อสอบจริง A-Level คณิตศาสตร์ประยุกต์ 1 เรื่องเรขาคณิตวิเคราะห์และภาคตัดกรวย (ปี 66)

ให้ $(a,b)$ เป็นจุดบนวงรี $\displaystyle \frac{x^2}{2} + \frac{y^2}{3} = 1$
ถ้าระยะห่างระหว่างจุด $(a,b)$ กับจุด $\left(0,-\frac{5}{4}\right)$ เท่ากับระยะระหว่างจุด $(a,b)$ กับเส้นตรง $y=-\frac{3}{4}$
แล้วค่าของ $b$ เท่ากับเท่าใด

$-3$
$\displaystyle -\frac{3}{2}$
$\displaystyle -\frac{3}{4}$
$\displaystyle \frac{3}{2}$
$3$

วิธีทำ

เนื่องจากระยะห่างระหว่างจุด $(a,b)$ กับจุด $\left(0,-\frac{5}{4}\right)$
เท่ากับระยะระหว่างจุด $(a,b)$ กับเส้นตรง $y=-\frac{3}{4}$ (หรือเส้นตรง $\displaystyle 0 \cdot x + 1 \cdot y + \frac{3}{4} = 0$ )
จะได้ว่า

\begin{align*} \sqrt{\left(a-0\right)^2+\left(b-\left(-\frac{5}{4}\right)\right)^2}\ &=\ \frac{\left|0(a)+1(b)+\displaystyle\frac{3}{4}\right|}{\sqrt{0^2+1^2}} \\ \sqrt{a^2+\left(b+\frac{5}{4}\right)^2}\ &=\ \left|b+\displaystyle\frac{3}{4}\right| \\ \left(\sqrt{a^2+\left(b+\frac{5}{4}\right)^2}\right)^2\ &=\ \left(\left|b+\displaystyle\frac{3}{4}\right|\right)^2 \\ a^2+\left(b^2 +2 \cdot b \cdot \frac{5}{4} + \left(\frac{5}{4}\right)^2\right) \ &=\ b^2 +2 \cdot b \cdot \frac{3}{4} + \left(\frac{3}{4}\right)^2 \\ a^2 \ &=\ - b - 1 \end{align*}

เนื่องจาก $(a,b)$ เป็นจุดบนวงรี จะได้ว่า $\displaystyle \frac{a^2}{2} + \frac{b^2}{3} = 1$ นั่นคือ $3a^2 + 2b^2 = 6$
และนำ $a^2 = -b-1$ ไปแทนในสมการ $3a^2 + 2b^2 = 6$ จะได้ว่า

\begin{align*} \\ 3(-b-1) + 2 b^2\ &=\ 6 \\ 2b^2 - 3b - 9\ &=\ 0 \\ (2b + 3)(b - 3)\ &=\ 0 \\ b\ &=\ -\frac{3}{2}, 3 \end{align*}

จัดรูปสมการวงรี $\displaystyle \frac{x^2}{2} + \frac{y^2}{3} = 1$ ให้อยู่ในรูปมาตรฐานได้เป็น $\displaystyle \frac{x^2}{(\sqrt{2})^2} + \frac{y^2}{(\sqrt{3})^2} = 1$
แสดงว่า $-\sqrt{2} < a < \sqrt{2}$ และ $-\sqrt{3} < b < \sqrt{3}$
ดังนั้น $\displaystyle b = -\frac{3}{2}$

ตอบ ข้อ 2. $\displaystyle -\frac{3}{2}$