สรุปเนื้อหา ตรรกศาสตร์

ตรรกศาสตร์คืออะไร ?

ตรรกศาสตร์ (Logic) คือ แขนงหนึ่งของคณิตศาสตร์ที่ว่าด้วยการใช้เหตุผลและหลักการคิดเชิงตรรกะ เพื่อช่วยให้เราตรวจสอบความถูกต้องของประโยคหรือข้อความได้อย่างแม่นยำ ถือเป็นพื้นฐานสำคัญของคณิตศาสตร์ คอมพิวเตอร์ และแม้แต่การใช้เหตุผลในชีวิตประจำวัน แล้วถ้าจะเริ่มเรียนตรรกศาสตร์ ควรจะรู้อะไรก่อน มาดูกันเลยย

ประพจน์ (Statement)

ประพจน์ คือ ข้อความที่สามารถบอกได้ว่า จริง $(T)$ หรือ เท็จ $(F)$ อย่างใดอย่างหนึ่ง
ตัวอย่างประพจน์:

$2 + 3 = 5$ เป็นจริง $(T)$
กรุงเทพฯ เป็นเมืองหลวงของประเทศไทย เป็นจริง $(T)$
$5$ เป็นเลขคู่ เป็นเท็จ $(F)$

โดยจะใช้ตัวอักษร $p,\ q,\ r$ เป็นสัญลักษณ์แทนประพจน์

ไม่ใช่ประพจน์ คือ ประโยคที่ไม่สามารถบอกได้ว่าเป็นจริงหรือเท็จ
ตัวอย่างไม่ใช่ประพจน์:

วันนี้กินอะไร
วันนี้อากาศดี

การเชื่อมประพจน์

การเชื่อมประพจน์ คือการเอาประโยคมาเชื่อมกัน โดยการใช้ตัวเชื่อม:

$\land$ (และ): ถ้ามี เท็จ $(F)$ แค่ 1 ตัว ให้เป็น เท็จ $(F)$ ทั้งหมด
$\vee$ (หรือ): ถ้าเป็น จริง $(T)$ แค่ 1 ตัว ให้เป็น จริง $(T)$ ทั้งหมด
$\rightarrow$ (ถ้า...แล้ว...): เป็น เท็จ $(F)$ ก็ต่อเมื่อ $p$ เป็นจริง $(T)$ และ $q$ เป็นเท็จ $(F)$ เท่านั้น
$\leftrightarrow$ (...ก็ต่อเมื่อ...): ถ้าประพจน์เหมือนกัน จะเป็นจริง $(T)$
$\sim$ (ไม่, นิเสธ): ค่าประพจน์ที่ตรงข้ามกัน

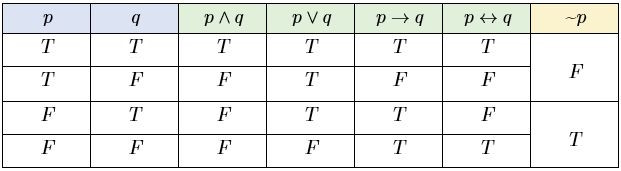
วิธีการหาค่าความจริงของประพจน์

การหาค่าความจริงของประพจน์ หมายถึง การพิจารณาว่าประโยคหรือข้อความนั้นเป็น จริง $(T)$ หรือ เท็จ $(F)$ โดยอาศัยหลักตรรกศาสตร์ โดยกำหนด $p$ : จริง, $q$ : จริง, $r$ : เท็จ, $s$ : เท็จ

\begin{align*} \sim p \vee (q \land s) &= F \vee (T \land F) \\ &= F \vee F \\ &= F \end{align*}

\begin{align*} (q \rightarrow r) \land \sim s &= (T \rightarrow F) \land T \\ &= F \land T \\ &= F \end{align*}

\begin{align*} (\sim r \rightarrow \sim s) \land (p \vee \sim q) &= (T \rightarrow T) \land (T \vee F) \\ &= T \land T \\ &= T \end{align*}

ตารางค่าความจริง

ตารางค่าความจริงคือตารางที่ใช้แสดงค่าความจริงของประพจน์ทั้งหมดที่เป็นไปได้ โดยใช้ตัวเชื่อมตรรกศาสตร์
ตัวอย่างการสร้างตารางค่าความจริงของ $(p \vee q) \rightarrow \sim p$

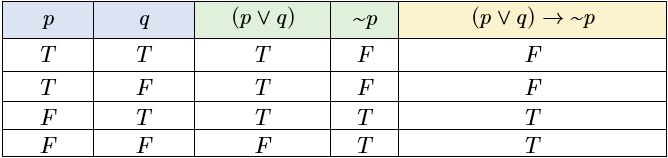
สัจนิรันดร์

สัจนิรันดร์คือประพจน์ที่เป็นจริงเสมอ ไม่ว่าค่าความจริงของตัวแปรจะเป็นอะไร
ถ้าสามารถทำให้ประพจน์เป็นเท็จได้ ประพจน์นั้นจะไม่ใช่สัจนิรันดร์

สมมูล

ประพจน์ที่สมมูลกัน คือ ประพจน์ที่ให้ค่าความจริงเหมือนกันทุกกรณีและสามารถใช้แทนกันได้ ในตรรกศาสตร์ใช้
แทนสัญลักษณ์ $\equiv$

ซึ่งถ้า $p$ เป็นจริง จะแทนด้วยสัญลักษณ์ $p \equiv T$

ถ้า $q$ เป็นจริง จะแทนด้วยสัญลักษณ์ $q \equiv T$

ถ้า $p$ มีค่าความจริงเหมือนกันกับ $q$ แสดงว่า $p$ สมมูลกับ $q$ จะแทนด้วยสัญลักษณ์ $p\equiv q$

รูปแบบประพจน์ที่สมมูลกัน

\begin{align*} p \rightarrow q &\equiv \sim p \vee q \\ p \rightarrow q &\equiv \sim q \rightarrow \sim p \\ \sim (p \vee q) &\equiv \sim p \land \sim q \\ \sim (p \land q) &\equiv \sim p \vee \sim q \end{align*}

การอ้างเหตุผล

คือเหตุการณ์หลายๆเหตุ ที่ทำให้เกิดผลลัพธ์ แล้วคิดว่าสมเหตุสมผลไหม การอ้างเหตุผลจะประกอบด้วย

เหตุหรือสิ่งที่กำหนดให้
ผลหรือข้อสรุป

ตัวอย่าง ถ้า ${(p}_1\land p_2\land p_3)\rightarrow q$ เป็นสัจนิรันดร์ หมายถึง การอ้างเหตุผลนั้นสมเหตุสมผล

ถ้า ${(p}_1\land p_2\land p_3)\rightarrow q$ ไม่เป็นสัจนิรันดร์ หมายถึง การอ้างเหตุผลนั้นไม่สมเหตุสมผล

ประโยคเปิด

คือประโยคที่มีตัวแปรอยู่ แต่ยังไม่นับว่าเป็นประพจน์ เราสามารถทำให้เป็นประพจน์ได้โดยใส่ตัวบ่งปริมาณเข้าไป

ตัวบ่งปริมาณ

คือตัวที่เอาไปใส่หน้าประโยคเปิดเพื่อกำหนดขอบเขตให้ตัวแปร จะมี 2 ตัว

ตัวบ่งปริมาณ ทั้งหมด ( $\forall x$ )
$\forall x P(x)$ หมายถึง $x$ ทุกตัวใน $\mathcal{U}$ เงื่อนไข $P$
ตัวบ่งปริมาณ บางตัว ( $\exists x$ )
$\exists x P(x)$ หมายถึง มี $x$ อย่างน้อย 1 ตัวใน $\mathcal{U}$ เงื่อนไข $P$

ข้อสังเกตุ
$\forall x[P(x)]$ เป็นจริง เมื่อ $x$ ทุกตัว แทนแล้ว $P(x)$ เป็นจริงหมดทุกตัว
$\forall x[P(x)]$ เป็นเท็จ เมื่อมี $x$ อย่างน้อย $1$ ตัว แทนแล้ว $P(x)$ เป็นเท็จ
$\exists x[P(x)]$ เป็นจริง เมื่อมี $x$ อย่างน้อย $1$ ตัว แทนแล้ว $P(x)$ เป็นจริง
$\exists x[P(x)]$ เป็นเท็จ เมื่อ $x$ ทุกตัว แทนแล้ว $P(x)$ เป็นเท็จหมดทุกตัว

ตัวอย่าง

1. จงหาค่าความจริงของ $\forall x[(x<0)\rightarrow(x^2>0)]$ โดยกำหนดให้ $\mathcal{U}=[{-1,\ 0,\ 1}]$

\begin{align*} x=-1 ; (-1<0)\rightarrow(1>0)\\ \ T\ \ \ \ \rightarrow\ \ \ \ \ T\ \ \ \ \equiv\ \ \ T\\ x=0 ; (0<0)\rightarrow(0>0)\\ F\ \rightarrow\ \ \ F\ \ \ \ \ \ \ \equiv\ \ \ T\\ x=1 ; (1<0)\rightarrow(1>0)\\ \ \ F\ \ \ \rightarrow\ \ \ T\ \ \ \ \equiv\ T \end{align*}

ประพจน์ทุกตัวเป็นจริง คำตอบคือ จริง

2. จงหาค่าความจริงของ $\exists x[(x<0)\land(x-1=0)]$ โดยกำหนดให้ $\mathcal{U}=[{-1,\ 0,\ 1}]$

\begin{align*} x=-1 ; (-1<0)\land(-1-1)=0\\ T\ \ \ \ \ \land\ \ \ \ \ \ \ F\ \ \ \ \ \ \ \ \equiv\ F\\ x=0 ; (0<0)\land(0-1)=0\\ \ \ \ \ \ F\ \ \ \land\ \ \ \ F\ \ \ \ \ \ \ \ \ \equiv\ F\\ x=1 ; (1<0)\land(1-1)=0\\ \ \ \ \ \ F\ \ \ \ \land\ \ \ \ T\ \ \ \ \ \ \ \ \equiv\ F \end{align*}

ไม่มี $x$ สักตัวที่ทำให้เป็นจริง คำตอบคือ เท็จ