สวัสดีคร้าบบ^^ โพสต์นี้พี่หมอแม็คจะมาพูดเกี่ยวกับจำนวนจริง ซึ่งเรื่องนี้เป็นพื้นฐานสำคัญถือว่าเป็นหัวใจหลักในการคำนวณ และต้องนำเรื่องนี้ไปประยุกต์ใช้ต่ออีกหลายเรื่อง พี่หมอแม็คได้สรุปเนื้อหาไว้ในโพสต์นี้โพสต์เดียวแล้วนะครับ นอกจากนี้ยังมีเทคนิคการทำข้อสอบเล็ก ๆ น้อย ๆ มาฝากกันคั้บบ

โครงสร้างของจำนวนจริง

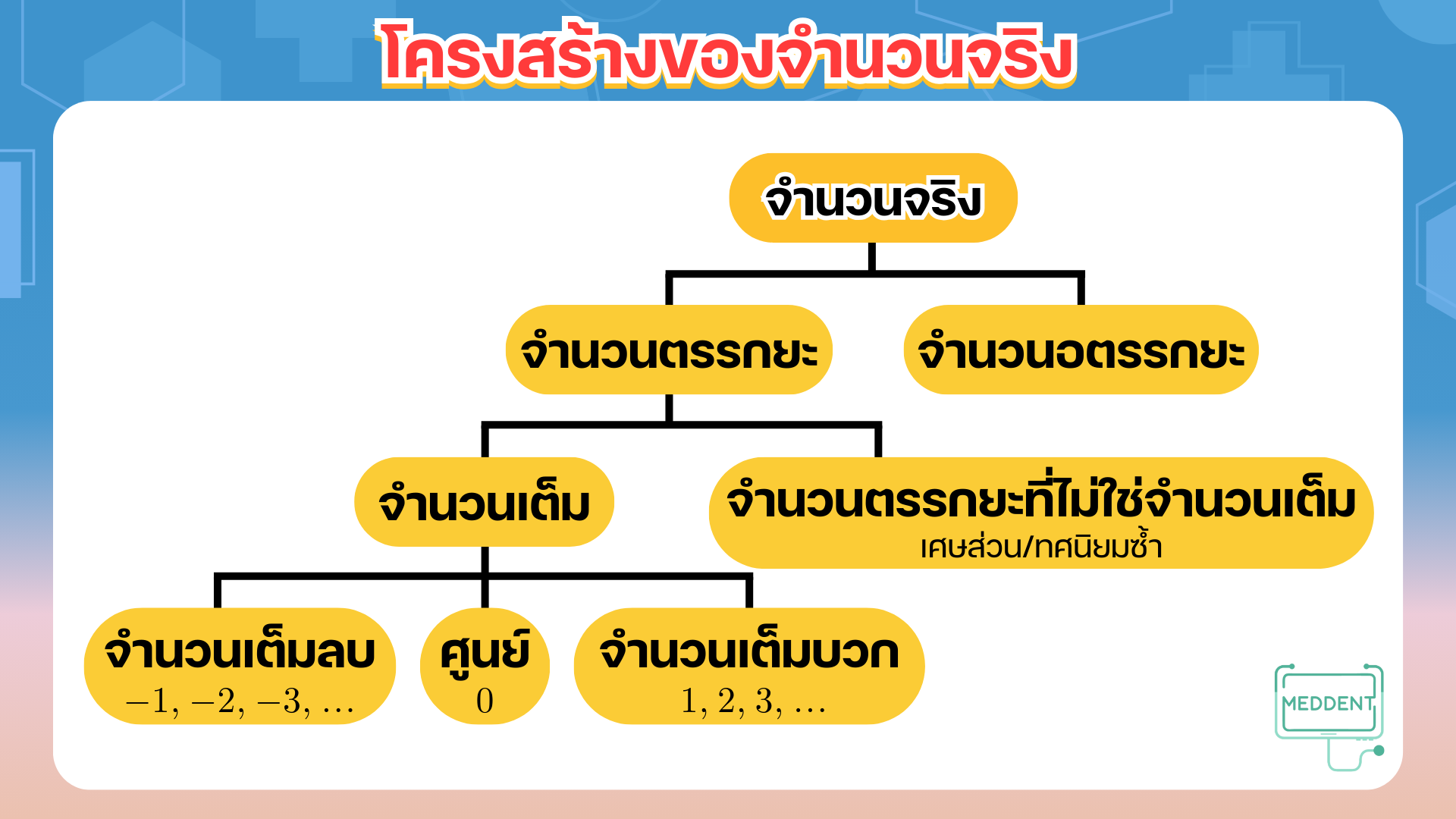
จำนวนจริง (real number) ประกอบไปด้วยจำนวนตรรกยะและจำนวนอตรรกยะ
จำนวนตรรกยะ: จำนวนที่เขียนในรูปเศษส่วนได้ เช่น $\displaystyle 7,\ 0,\ -5,\ \frac{1}{2},\ \frac{1}{3}$
จะเห็นว่า จำนวนตรรกยะอาจเป็นจำนวนเต็ม หรือเศษส่วน หรือทศนิยมซ้ำก็ได้
จำนวนอตรรกยะ: จำนวนที่เขียนในรูปเศษส่วนไม่ได้ เช่น $\sqrt{2} \approx 1.414,\ \sqrt{3} \approx 1.732,\\ \sqrt{5} \approx 2.236,\ \pi \approx 3.142$ เป็นต้น

สมบัติของจำนวนจริง

จำนวนจริงมีสมบัติภายใต้การบวก ( $+$ ) และการคูณ ( $\cdot$ ) ต่อไปนี้

พหุนาม

พหุนาม (polynomial) นิยมเขียนด้วย $p(x),\ q(x)$ หรือ $r(x)$ คือ การรวมของพจน์ในรูป

\begin{align*} a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0 \end{align*}

เมื่อ $n$ เป็นจำนวนเต็มที่ไม่เป็นลบ ซึ่งเรียกว่า ดีกรี (degree) ของ $p(x)$ เขียนแทนด้วย $\deg (p(x))$
โดยที่ $a_0, a_1, \ldots, a_n$ เป็นจำนวนจริง และ $a_n \neq 0$ จะเรียกว่า สัมประสิทธิ์ (coefficient)

ตัวอย่างของพหุนาม

$x^3-3x^2+4x-1$ เป็นพหุนามดีกรี $3$
$6x^7$ เป็นพหุนามดีกรี $7$

การบวกและลบพหุนาม

การบวก/ลบพหุนามสามารถนำพจน์คล้ายกันบวก/ลบได้เลย แต่ถ้าไม่มีพจน์ที่คล้ายกันให้ค้างไว้นะคับ

การคูณพหุนาม

การคูณพหุนามให้คูณกระจายแต่ละพจน์เข้าอีกวงเล็บ แล้วนำมาบวกหรือลบตามปกติได้เลยครับ

การหารพหุนาม

ขั้นตอนวิธีการหารพหุนาม

\begin{align*} \text{ตัวตั้ง} &= \text{ตัวหาร} \cdot \text{ผลหาร} + \text{เศษเหลือ} \\ a(x) &= b(x) \cdot q(x) + r(x) \end{align*}

เมื่อหาร $a(x)$ ด้วย $b(x)$ ทำให้ได้ผลหาร $q(x)$ และเศษเหลือ $r(x)$ ซึ่งสามารถเกิดได้ 2 กรณี คือ
กรณีที่ 1 $\deg(r(x)) \leq \deg(b(x))$ นั่นคือ ดีกรีของเศษเหลือน้อยกว่าดีกรีผลหาร
กรณีที่ 2 เศษเหลือ $r(x) = 0$ (ในที่นี้จะเป็นการหารลงตัวนั่นเอง)

การแยกตัวประกอบของพหุนาม
จากขั้นตอนวิธีการหารพหุนาม ในกรณีที่เป็นการหารลงตัว นั่นคือ $a(x) = b(x) \cdot q(x)$
แล้วจะกล่าวว่า $b(x)$ และ $q(x)$ เป็นตัวประกอบของ $a(x)$ สำหรับการแยกตัวประกอบพหุนามทำได้หลายแบบขึ้นอยู่กับความเหมาะสมและเทคนิค ซึ่งพี่แม็คสรุปให้น้องตามรูปนี้ค้าบบ

สำหรับทฤษฎีบทที่พี่แม็คจะพูดถึงต่อไปนี้ได้แก่ ทฤษฎีบทเศษเหลือ และทฤษฎีบทตัวประกอบ ทั้ง 2 ทฤษฎีบทนี้จะเป็นตัวช่วยในการแยกตัวประกอบของพหุนามให้ง่ายยิ่งขึ้น โดยพิจารณาจากตัวประกอบของพจน์ที่เป็นค่าคงที่ อีกทั้งสามารถแยกตัวประกอบของพหุนาที่ดีกรีมากกว่า $2$ ได้ง่ายยิ่งขึ้นอีกด้วยค้าบบ

สมการพหุนาม

สมการพหุนาม คือ สมการที่เขียนในรูป

\begin{align*} a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0 = 0 \end{align*}

คำตอบ (solution) ของสมการพหุนาม คือ จำนวนจริง $c$ ที่ทำให้ $p(c) = 0$ (นั่นคือ แทนค่า $x$ ด้วย $c$ แล้วสมการเป็นจริง)

การแก้สมการพหุนามสามารถทำได้หลายวิธีกันเลย อย่างเช่น ใช้การแยกตัวประกอบของพหุนามที่พี่แม็คได้พูดถึงมาแล้ว ซึ่งจะได้ผลคูณของตัวประกอบเท่ากับ $0$ แสดงว่า ต้องมีตัวประกอบที่มีค่าเท่ากับ $0$ นั่นคือ จับแต่ละวงเล็บไปเท่ากับ $0$ แล้วหาคำตอบของแต่ละสมการออกมาได้เลยคับ หรืออีกวิธีนึงถ้าเป็นสมการพหุนามดีกรี $2$ โดยใช้สูตร สามารถหาคำตอบของสมการ $ax^2 + bx + c = 0$ ได้คือ $\displaystyle x = \frac{-b\pm\sqrt{b^2-4ac}}{2a}$ นั่นเองค้าบบ

การไม่เท่ากันของจำนวนจริง

ความสัมพันธ์ที่เกี่ยวข้องกับการไม่เท่ากันของจำนวนจริง ได้แก่ ความสัมพันธ์มากกว่า มากกว่าหรือเท่ากับ น้อยกว่า น้อยกว่าหรือเท่ากับ ไม่เท่ากับ
สมบัติการไม่เท่ากันของจำนวนจริง
ให้ $a, b$ และ $c$ เป็นจำนวนจริง

ถ้า $a < b$ และ $b < c$ แล้ว $a < c$
ถ้า $a < b$ แล้ว $a+c < b+c$
ถ้า $a+c < b+c$ แล้ว $a < b$
ถ้า $a < b$ และ $c > 0$ แล้ว $ac < bc$
ถ้า $ac < bc$ และ $c > 0$ แล้ว $a < b$
ถ้า $a < b$ และ $c < 0$ แล้ว $ac > bc$
ถ้า $ac < bc$ และ $c < 0$ แล้ว $a > b$

ช่วง

ช่วง (interval) คือ เซตของจำนวนจริงที่กำหนดค่าพิจารณาไว้อย่างต่อเนื่อง

อสมการพหุนาม

อสมการพหุนาม คือ ประโยคที่แสดงถึงความไม่เท่ากัน โดยใช้เครื่องหมาย $>, \geq, <, \leq$ หรือ $\neq$

การแก้อสมการพหุนามสามารถทำได้โดยใช้การแยกตัวประกอบพหุนามที่พี่แม็คได้พูดถึงมาแล้วได้เลยครับ แล้วหลังจากนั้นให้พิจารณาบนช่วงที่สอดคล้องกับความสัมพันธ์ นั่นคือ แบ่งช่วง $+/-/+$ นั่นเองคร้าบบ ถ้าเป็นความสัมพันธ์มากกว่าให้ตอบช่วง $+$ และถ้าเป็นความสัมพันธ์น้อยกว่าให้ตอบช่วง $-$ ครับ

ค่าสัมบูรณ์

ค่าสัมบูรณ์ (absolute value) ของจำนวนจริง $x$ เขียนแทนด้วย $\left|x\right|$ กำหนดโดย

\begin{align*} \left | x \right |= \begin{cases} x & \text{เมื่อ } x \geq 0 \\-x & \text{เมื่อ } x < 0 \end{cases} \end{align*}

ข้อสอบจริง A-Level คณิตศาสตร์ประยุกต์ 1 เรื่องจำนวนจริง (ปี 66)

ให้ $p(x) = x^3 + (k-1)x^2 - k^3$ เมื่อ $k$ เป็นจำนวนจริงลบ ถ้าเศษเหลือจากการหาร $p(x)$ ด้วย $x-3$ เท่ากับ $18$ แล้วเศษเหลือจากการหาร $p(x)$ ด้วย $2x+1$ เท่ากับเท่าใด

$3$
$18$
$22$
$\displaystyle \frac{207}{8}$
$\displaystyle \frac{209}{8}$

วิธีทำ เนื่องจากเศษเหลือจากการหาร $p(x)$ ด้วย $x-3$ เท่ากับ $18$ โดยทฤษฎีบทเศษเหลือ จะได้ว่า

\begin{align*} p(3) &= 18 \\ (3)^3 + (k-1)(3)^2 - k^3 &= 18 \\ 27 + (9k-9) - k^3 &= 18 \\ 9k - k^3 &= 0 \\ k(9-k^2) &= 0 \\ k(3-k)(3+k) &= 0 \\ k &= 0,\ 3,\ -3 \end{align*}

ดังนั้น $k=-3$
เพราะฉะนั้น $p(x) = x^3 - 4x^2 + 27$ ทำให้เศษเหลือจากการหาร $p(x)$ ด้วย $2x+1$ เท่ากับ

\begin{align*} p\left(-\frac{1}{2}\right) &= \left(-\frac{1}{2}\right)^3 - 4\left(-\frac{1}{2}\right)^2 +27\\ &= -\frac{1}{8} - 4\left(\frac{1}{4}\right) + 27\\ &= -\frac{1}{8} + 26\\ &= \frac{208-1}{8}\\ &= \frac{207}{8} \end{align*}

ตอบ ข้อ 4. $\displaystyle \frac{207}{8}$