สรุปเนื้อหา เซต

ถ้าน้อง ๆ เพิ่งขึ้น ม.4 เรื่องแรกที่ต้องเรียนในคณิตศาสตร์คือ เรื่องเซตซึ่งเป็นพื้นฐานสำคัญของหลายบทใน ม.ปลาย ถ้าเข้าใจเรื่องนี้ดี จะช่วยให้ต่อยอดไปบทอื่นได้ไม่ยาก แต่ถ้าอ่านแล้วยังงงไม่ต้องกังวลไปน้าา พี่แม็คสรุปเนื้อหาพร้อมตัวอย่างโจทย์มาให้แล้ว ถ้าพร้อมแล้วไปลุยกันเลย!!

เซตคืออะไร ?

เซต ก็คือ กลุ่มของอะไรบางอย่าง ที่เราสามารถบอกได้ชัดๆ ว่าสิ่งนั้นอยู่ในกลุ่มหรือเปล่า
เช่น เซตของผลไม้ในตะกร้า = $\{ \text{แอปเปิ้ล}, \text{กล้วย}, \text{ส้ม}, \text{มะม่วง} \}$
และ เซตของเลขคู่ที่มากกว่า 0 แต่น้อยกว่า 10 = $\{2, 4, 6, 8\}$

** Tip: ลำดับสมาชิกไม่มีความสำคัญนะ **
เวลาเขียนเซต เราจะใส่สมาชิกของเซตไว้ใน $\{ \}$ ถ้าจะบอกว่าสิ่งไหนเป็นสมาชิกของเซต
เราจะใช้เครื่องหมาย $\in$ (เป็นสมาชิก) แต่ถ้าไม่อยู่ในเซต เราจะใช้เครื่องหมาย $\notin$ (ไม่เป็นสมาชิก)
เช่น 4 เป็นสมาชิกของเซตเลขคู่ที่มากกว่า 0 แต่น้อยกว่า 10 เขียนเป็น $4 \in \{2, 4, 6, 8\}$
แต่ 5 ไม่ใช่สมาชิกของเซตเลขคู่เต็มบวก ก็เขียนเป็น $5 \notin \{2, 4, 6, 8\}$

วิธีเขียนเซต

มี 2 วิธีหลักๆ ในการเขียนเซตคือ

1. เขียนแบบแจกแจงสมาชิก (บอกไปเลยว่าอะไรอยู่ในเซต)
   เช่น $\{1, 2, 3, 4, 5\}$
   
2. เขียนแบบบอกเงื่อนไข (อธิบายแทนที่จะไล่เรียงทุกตัว)
   เช่น $\{x \in \mathbb{N} \mid x < 10\}$ (x ต้องเป็นจำนวนนับ โดยที่ x น้อยกว่า 5)

ชนิดของเซต

• เซตว่าง คือ ไม่มีอะไรอยู่ในเซตเลย เช่น $\{\}$ หรือ $\emptyset$
• เซตจำกัด คือ เซตที่บอกจำนวนสมาชิกได้แน่นอน เช่น $\{1, 2, 3\}$
• เซตอนันต์ คือ เซตที่มีจำนวนสมาชิกนับไม่ถ้วน เช่น $\{1, 2, 3, \dots\}$
• เซตเอกภพสัมพัทธ์ $(U)$ คือ เซตที่กำหนดขอบเขตของสมาชิกในเซต
  $\mathbb{N}$ แทนเซตของจำนวนนับ
  $\mathbb{Z}$ แทนเซตของจำนวนเต็ม
  $\mathbb{Q}$ แทนเซตของจำนวนตรรกยะ
  $\mathbb{Q}^\prime$ แทนเซตของจำนวนอตรรกยะ
  $\mathbb{R}$ แทนเซตของจำนวนจริง
  $\mathbb{C}$ แทนเซตของจำนวนเชิงซ้อน

ตัวอย่างที่ 1

กำหนดให้ $U = \{-2, 0, 2, 4, 6, 8\}$ เป็นเอกภพสัมพัทธ์ $A = \{x \mid 0 < x \leq 6 \}$ และ $B = \{x \mid x < 6 \}$
เขียนเซต $A$ และ $B$ แบบแจกแจงสมาชิกจะได้ว่า $A = \{2, 4, 6\}$ และ $B = \{-2, 0, 2, 4\}$

สับเซต (Subset)

ถ้าเซต $A$ เป็นสับเซตของเซต $B$ หรือพูดง่ายๆ ว่า สมาชิกที่อยู่ใน $A$ ต้องอยู่ใน $B$ ทุกตัว จะเขียนว่า $A \subset B$ แต่ถ้า $A$ ไม่เป็นสับเซตของ $B$ (หมายถึงมีบางตัวใน $A$ ที่ไม่ได้อยู่ใน $B$) จะใช้สัญลักษณ์ $A \not \subset B$

**Tip: $\emptyset$ (เซตว่าง) เป็นสับเซตของทุกเซต และเรายังสามารถหาจำนวนสมาชิกทั้งหมดได้โดยใช้ $2^n$**

ตัวอย่างที่ 2

• $A = \{1, 2\}$
• $B = \{1, 2, 3, 5\}$
• $C = \{4, 5\}$

จะเห็นว่าสมาชิกใน $A$ อยู่ใน $B$ ทั้งหมด ดังนั้น $A \subset B$ แต่สมาชิกใน $A$ ไม่ได้อยู่ใน $C$ ทั้งหมด
ดังนั้น $A \not \subset C\$ และสับเซตทั้งหมดของ $A$ คือ $\emptyset$, $\{1\}$, $\{2\}$, $\{1, 2\}$

แผนภาพเวนน์ (Venn Diagram)

แผนภาพเวนน์คือ วิธีที่เราวาดรูปวงกลมเพื่อแสดงความสัมพันธ์ระหว่างเซตต่างๆ โดยใช้วงกลมแทนเซตๆ หนึ่ง ถ้าเซตนั้นมีสมาชิกที่เหมือนกันก็จะอยู่ในส่วนที่วงกลมซ้อนทับกัน ช่วยให้เห็นได้ชัดเจนว่าแต่ละเซตมีสมาชิกอะไรบ้าง อีกทั้งยังสามารถใช้ในการแก้โจทย์เกี่ยวกับการหาจำนวนสมาชิกในเซตได้อีกด้วย

การดำเนินการของเซต

การดำเนินการของเซตมี 4 แบบหลักๆ

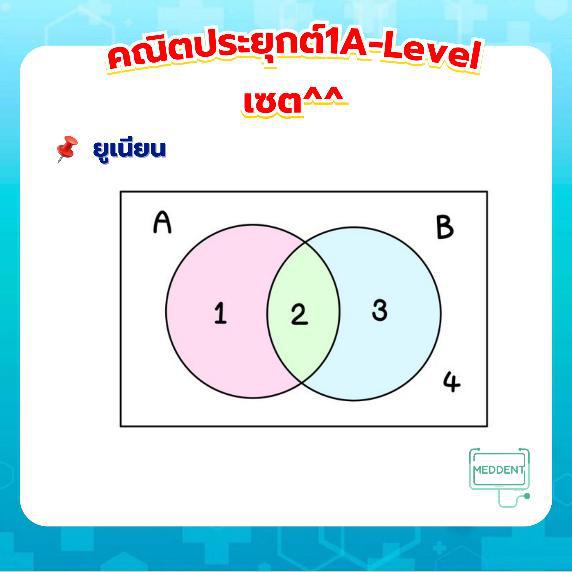
1. ยูเนียน $(A \cup B)$ คือการรวมสมาชิกที่อยู่ใน $A$ กับ $B$
   เช่น $A = \{1, 2\}$ และ $B = \{2, 3\}$ จะได้ว่า $A \cup B = \{1, 2, 3\}$
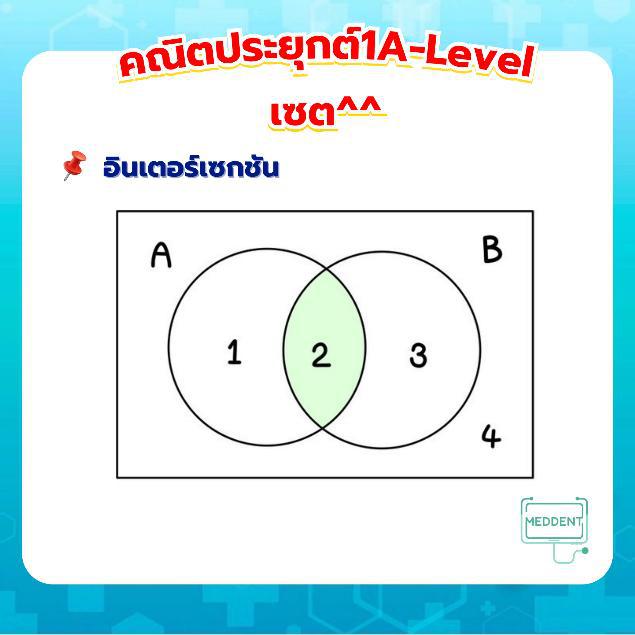
2. อินเตอร์เซกชัน $(A \cap B)$ คือการเอาเฉพาะสมาชิกที่ $A$ และ $B$ มีเหมือนกัน
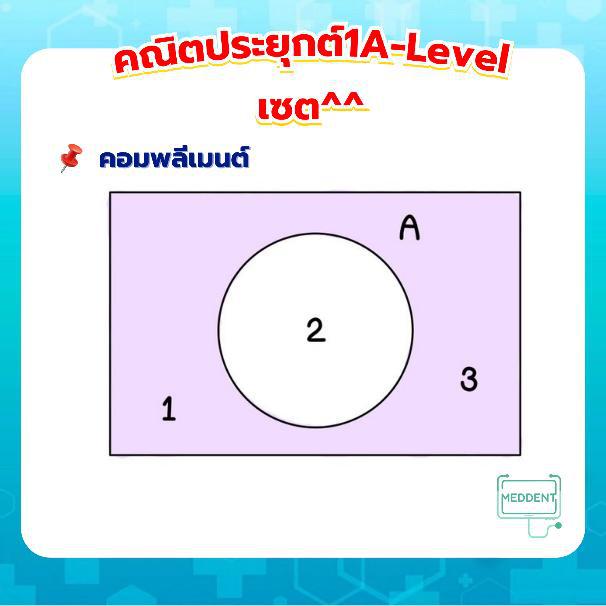
   เช่น $A = \{1, 2\}$ และ $B = \{2, 3\}$ จะได้ว่า $A \cap B = \{2\}$ (แค่ตัวที่ซ้ำกัน)
3. คอมพลีเมนต์ $(A')$ คือทุกอย่างที่ไม่ใช่เซต $A$
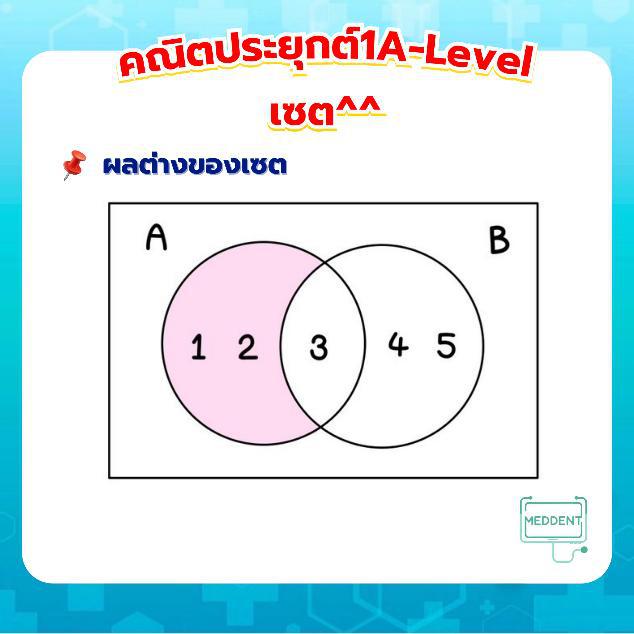
   ถ้าเซตเอกภพสัมพัทธ์คือ $\{1, 2, 3\}$ และ $A = \{2\}$ จะได้ว่า $A' = \{1, 3\}$ (ทุกอย่างที่เหลือ)
4. ผลต่างของเซต $(A - B)$ คือสมาชิกที่อยู่ใน $A$ แต่ไม่อยู่ใน $B$
   เช่น $A = \{1, 2, 3\}$ และ $B = \{3, 4, 5\}$ จะได้ว่า $A - B = \{1, 2\}$ (เพราะ 3, 4, 5 มีใน $B$ แล้ว)

การนับจำนวนสมาชิกของเซต

ถ้าให้ $n(A)$ แทนจำนวนสมาชิกของเซต $A$ และ $n(B)$ แทนจำนวนสมาชิกของเซต $B$
สูตรที่ใช้บ่อยคือ

1. $n(A) = n(U) - n(A')$
2. $n(A - B) = n(A) - n(A \cap B)$
3. $n(A \cup B) = n(A) + n(B) - n(A \cap B)$
4. $n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(A \cap C) - n(B \cap C) + n(A \cap B \cap C)$

ตัวอย่างที่ 3

สำรวจคน 20 คน ที่ต้องชอบดูหนังหรือฟังเพลงอย่างน้อย 1 อย่าง ถ้ามีคนชอบดูหนัง 12 คน และมีคนชอบฟังเพลง 14 คน จงหาจำนวนคนที่ชอบดูหนังและฟังเพลง
วิธีทำ

ตัวอย่างที่ 4

จากการสอบถามวิชาเรียนที่นักเรียนชอบ จำนวน 180 คน พบว่า มีคนชอบวิชาคณิตศาสตร์ 86 คน ชอบวิทยาศาสตร์ 87 คน ชอบภาษาอังกฤษ 70 คน ชอบคณิตศาสตร์และวิทยาศาสตร์ 31 คน ชอบวิทยาศาสตร์และภาษาอังกฤษ 27 คน ชอบคณิตศาสตร์และภาษาอังกฤษ 22 คน และ มี 5 คน ที่ไม่ชอบเรียนทั้ง 3 วิชา จงหาจำนวนนักเรียนที่ชอบทั้ง 3 วิชา จงหาจำนวนนักเรียนที่ชอบทั้ง 3 วิชา
วิธีทำ

กำหนดให้

คนที่ชอบคณิตศาสตร์ เป็น $n(A)$

คนที่ชอบวิทยาศาสตร์ เป็น $n(B)$

คนที่ชอบภาษาอังกฤษ เป็น $n(C)$

คนที่ชอบเรียนอย่างน้อย1วิชา จะเป็น

จากสูตร

$n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(A \cap C) - n(B \cap C) + n(A \cap B \cap C)$

แทนค่า